Flat Crochet Mathematics

A friend of mine approached me with a very interesting problem where the intersection of many disciplines can come into play which would make way for an interesting exercise. She was knitting flat pieces of crochet, and noticed the fractal patterns that appear, and from the number of crochet examples she had in hand, she was experimenting with various techniques to see how the overall pattern would emerge. I myself didn't know much about knitting, but the mathematical aspects of the problem were very intriguing. There must be a method of breaking down the knitting process into a formula or set program, where a simple change of parameters can provide dramatic changes in the overall pattern.

After a brief google search I learned of certain terms used in the actual physical knitting of crochet, the chain, the simple crochet, and the slip stitch. The act of knitting these flat masterpieces of tapestry also always seem to emanate from the center. An interesting method of trying to define a simple algorithm of a pattern I thought could be used with cylindrical coordinates.

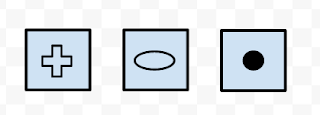
The cross can represent a single crochet, the oval a chain, and the dot a slip stitch

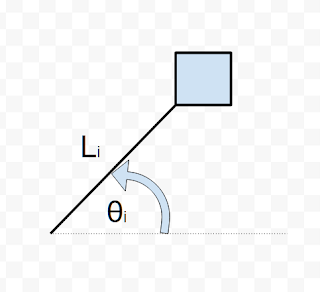
If the center of the tapestry can be considered the origin, then the generation of the pattern can emerge with the simple variables of angle, length from the origin, and the sequence of crotchet knots at the specified point on the flat plane.

A pattern can then be made by adding additional rules to each of the parameters, such as a formula which controls the radial length "L" to allow gaps based on it's position of angle, and how many concentric circles have already been made up to that point. The sequence of crochet parameters can also be connected to the formula of L and theta, to create patterns that are unique to create radial arms, of rows of concentric rings.

Once a set program could be made to show simulated results based on user input of those specific parameters, then one could see how the resulting patterns can emerge from scale and complexity.


Specific formulas for theta can be the following

2pi/No radial arms

The mathematical looping can be flattened by dividing up the 3D curves into individual curves that start at the very bottom to the very top.

Applying a Hessian to the parameterized curve can identify individual curves either sloping up or sloping down which can be quickly represented using simple 2D vectors.